Understanding Modspaces Visually
A lot of students in office hours seemed to be unsure of what a Modspace is and exactly what \(\mod m\) means (is it a function?) or how \(3 \equiv 18 \mod 15\). To start out, we need to talk about what a Modspace is. (Note: super mathy things that you should read about if you're interested are written in italics, ex: tropical math).
Consider the integers, \(\mathbb{Z}\). For integers, \(+\) is some operation called an 'addition' that takes in two numbers and adds them together. There is an additive identity \(0\) defined to be the number such that \(a + 0 = a\) and each number \(a\) has an additive inverse \(-a\), defined to be the number such that \(a + (-a) = 0\).
There's also some operation \(\times\) called a 'multiplication', for which there is a multiplicative identity \(1\) such that \(1 \times a = a\) for any number \(a\), and which distributes over addition, meaning \[c \times (a + b) = c \times a + c \times b \]
Super mathy people called Algebraists call structures with these properties commutative rings. It's a mathy structure to describe some collection of things that you can add and multiply, like we're used to. Modspaces define one of these structures on some smaller subset of \(\mathbb{Z}\). What happens if we take this structure and constrict its elements down from \({\dots -2, -1, 0, 1, 2 \dots }\) to something like \({0, 1, \dots m-1}\)? Well, we need to redefine addition and multiplication to be compatible with this change, and modspaces choose a very particular way of doing this.
When we write \(3 \equiv 18 \mod 15\), we don't mean that \(3 = 18\) in the integers. What we mean is that in the Modspace with \(m=15\), \(3\) is equivalent to \(18\). We can talk about defining an equivalence relationship for \(\mod 15\), called \(\sim\), which behaves like \(=\) in that it's reflexive (\( a \sim a\)), symmetric (\(a \sim b \Longleftrightarrow b \sim a\)), and transitive (\(a \sim b \land b \sim c \Longleftrightarrow a \sim c \)).
In the case of Modspaces, we define \(a\) and \(b\) to be equivalent (\(a \sim b \)), if \(a=b + k \times m \) for some \(k \in \mathbb{Z} \). This intuitively means that \(a \sim b\) if \(a\) and \(b\) are equivalent up to adding multiples of \(m\). Note that \(a,b,k,m\) are integers, \(=\) is the normal equivalence in the integers, and \(+\) and \(\times \) are the normal operations from the integers, so this equivalence class is defined in terms of operations on the integers.
What Modspaces do is take all of the integers and 'glue together' those which are equivalent with respect to \(\sim \). We bundle all these up into a single element of the Modspace, called an equivalence class. These classes are denoted as \([a]\), and can be vaguely understood as the collection of elements equivalent to it (\([a] \approx {b \mid a \sim b})\). Another way to understand this is as following: let's deal with \(\mod 15\) and imagine we draw out the number line in this specific way
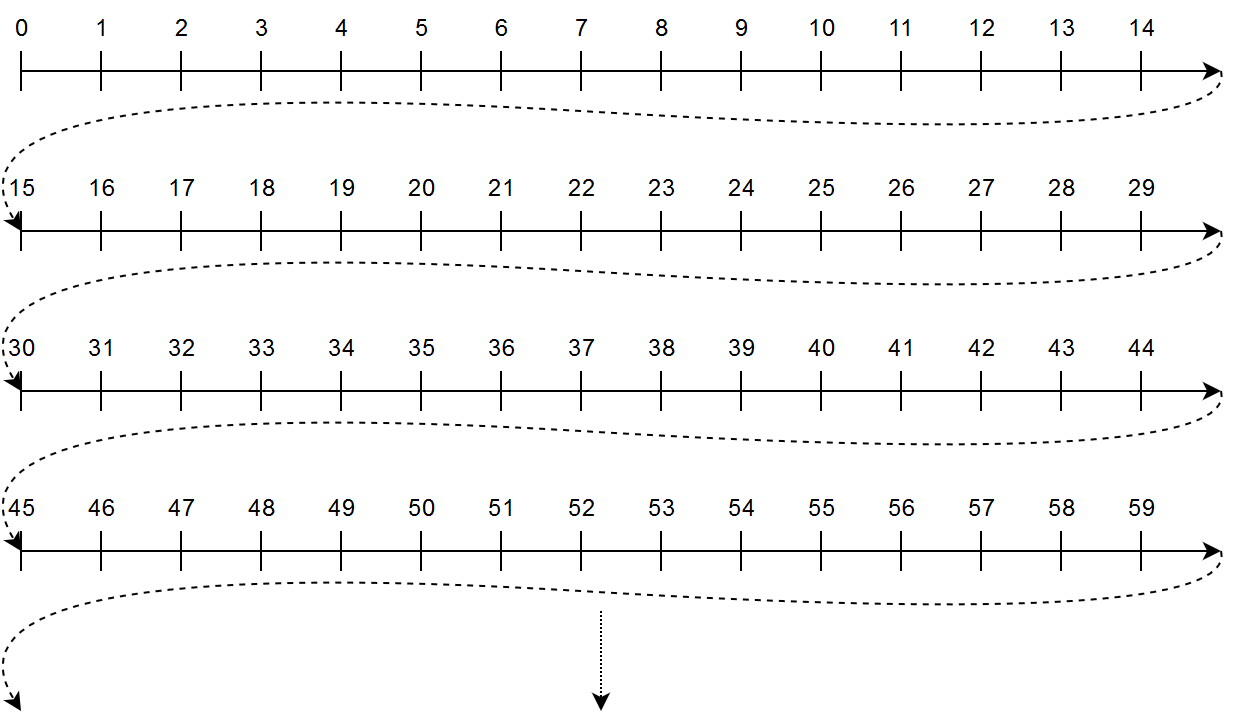
What we are doing when defining this equivalence class is collapsing these lines along the y-axis. This looks like the following:
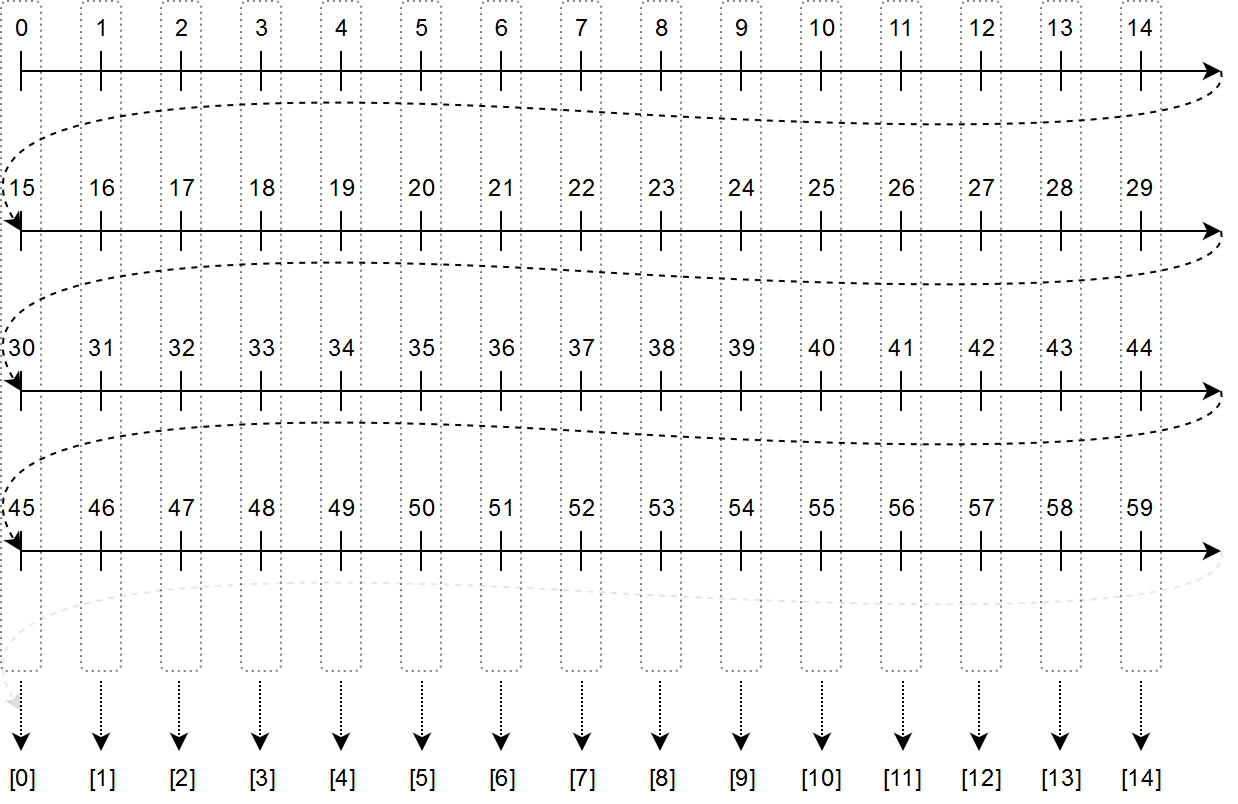
Now that we have a set of elements (all the \([a]\) for \(a \in {0, 1, \dots m}\)) we want to turn it into one of those mathy structures like the integers. In order to do so, we need to define an 'addition' and 'multiplication' that exhibit the properties we require.
To keep clear which multiplication/addition is which, I'll use the symbol \(\otimes\) and \(\oplus\) to denote the multiplication and addition respectively in \(\mod m\). We define these in the obvious way: $$ [a] \oplus [b] \sim [a + b] $$ $$ [a] \otimes [b] \sim [a \times b]$$
To add or multiply any two elements of the Modspace, we say simply look at the equivalence class of their integer sum/product. Simple right? (A good exercise is to check that our addition/multiplication \(\oplus\) and \(\otimes\) are well-defined, that is you get the same result regardless of which representatives of the equivalence class you choose).
Going back to this example, let's try to understand exactly what's happening: $$3 \equiv 18 \mod 15$$
Firstly, \(3,18 \mod 15\) represent the equivalence classes \([3]\) and \([18]\). As \([3] \equiv [3 + k \times m]\) and for \(k=1, 3+1\times 15 = 18\), then \([3]=[18]\) and \(3 \equiv 18 \mod 15\). We can also use our picture of the number line to see that 3 and 18 both get 'squished' down to the same number:
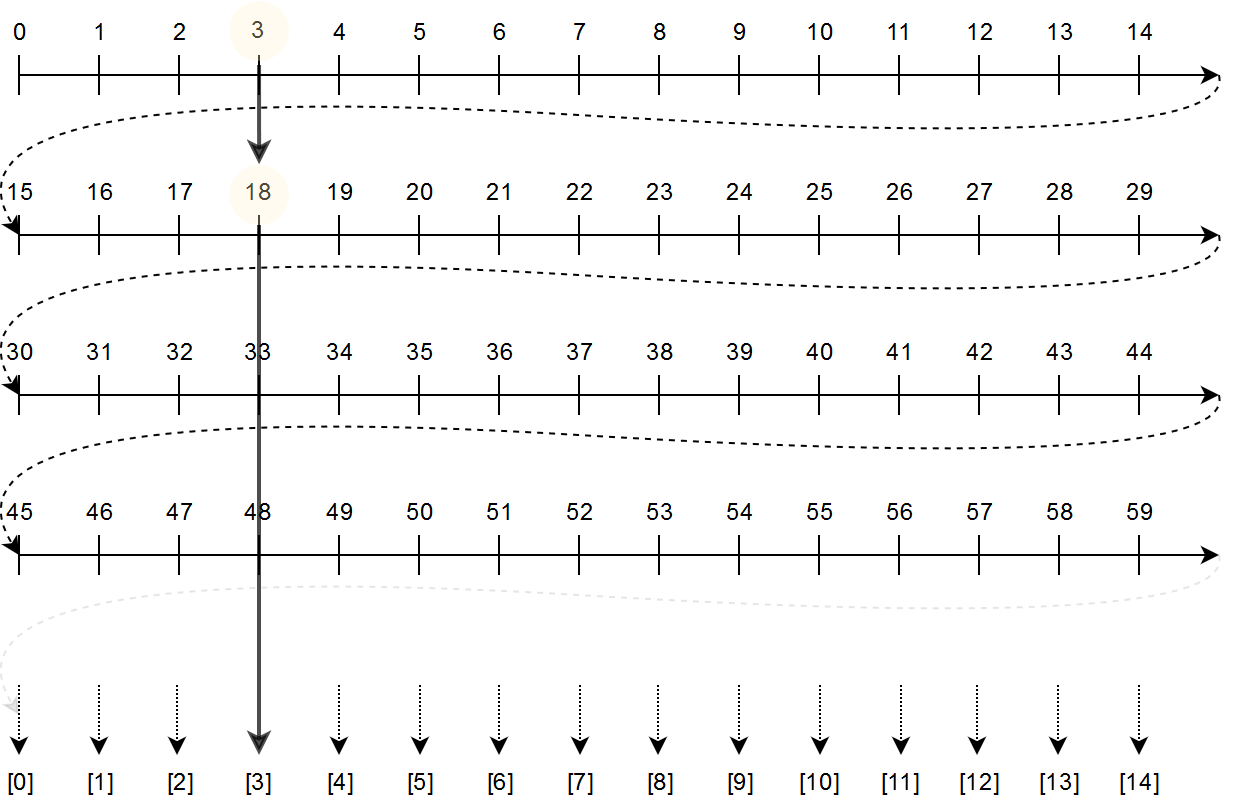
You can also understand how our definition of \(\oplus\) and \(\otimes\) works by looking at how an expression such as \(8 + 14 \equiv 7 \mod 15\). We simply jump along the number line (like we used to back in elementary school), and see that we end up landing on the equivalence class corresponding to \(7\):
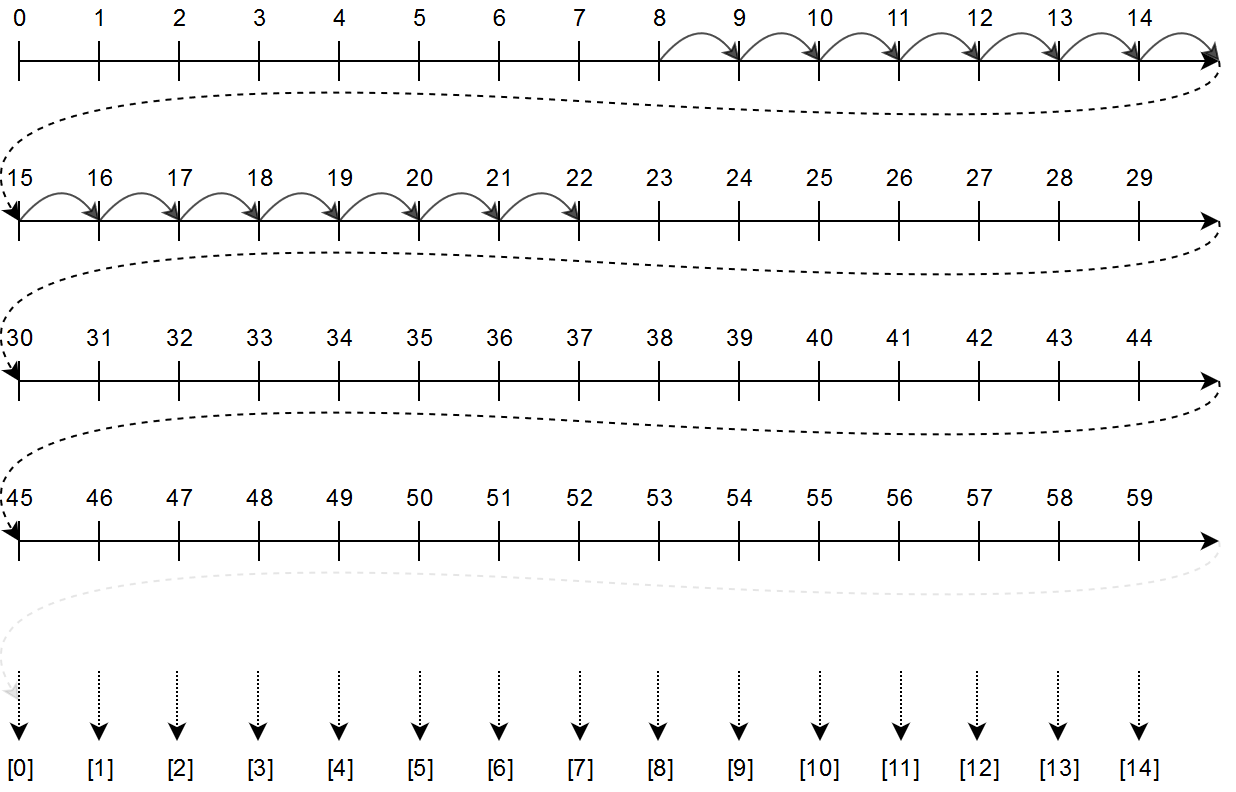
Not so bad, right?